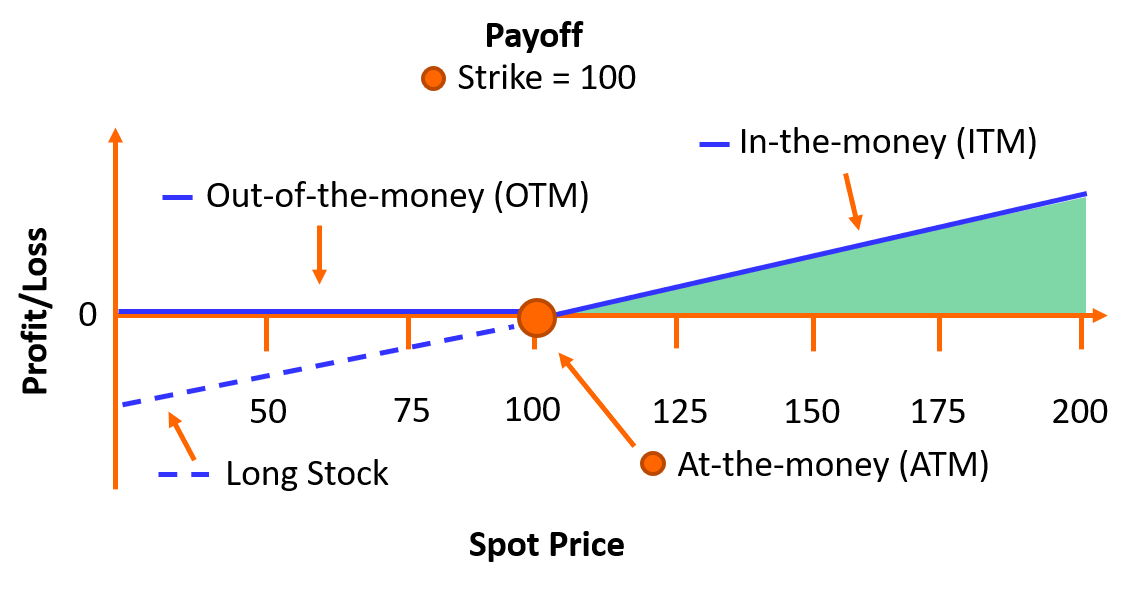
Optionsvärdering
Hur fungerar optioner? Vi hjälper dig med optionsvärdering och allt som hör till optionsprogram. Se exempel med Black–Scholes!
Den här artikeln ger dig en bakgrund till den berömda optionsformeln.
Black-Scholes-Mertons formeln för en köpoption lyder som följer:
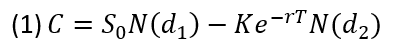
där C står för priset på en köpoption, S(0) är den initiella aktiekursen (tillgången), K är optionens lösenpris (tillgångens förutbestämda pris), r är den riskfria räntan, T är löptiden. N(d1) och N(d2) är kumulativa sannolikhetsfördelningsfunktionen, som specificeras enligt följande:
![bsformula2_3 (2) d1 = [ln(S0/K)+(r+(sigma^(2)/2)xT]/sigma^(1/T) (3) d2 =[ln(S0/K)+(r-(sigma^(2)/2)xT]/sigma^(1/T)](https://www.optionspartner.se/wp-content/uploads/2021/09/bsformula2_3.png)
där σ^2 är den underliggande tillgångens varians.

Låt oss nu ta ett praktiskt exempel på hur Black-Scholes-Merton-formeln används för att beräkna priset på alternativ A i vår presentation. Alternativ A är en ”European Long Call” och har följande egenskaper:
Aktievärde (S0)
100
Lösenpris (K)
100
Löptid (år) (T)
3
Riskfri ränta (e^(-rT)
0
Volatilitet (σ)
30 %
Som ett första steg, låt oss fortsätta med att beräkna ekv. (2) och (3):
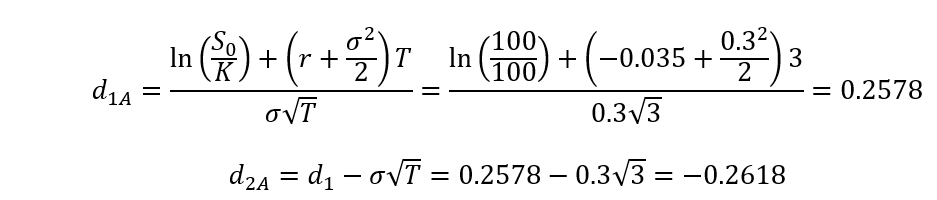
Slutligen har vi den ekv. (1) har följande form:
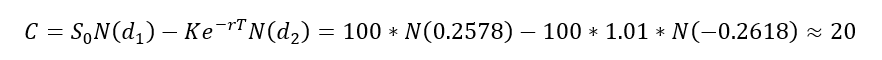
Således är priset för alternativ A cirka 20.
Värdera din option helt kostnadsfritt
Optionsvärdering på egen hand. Testa själv!
Ta mig till kalkylatorn