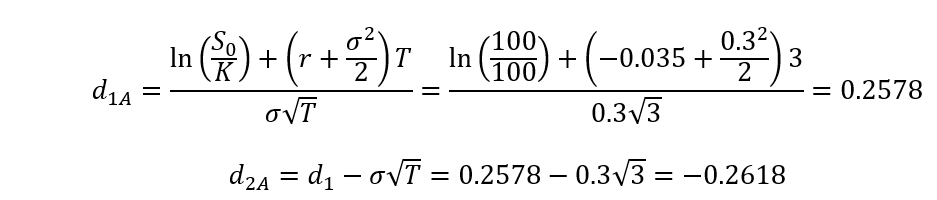Optionskalkylator
Enkelt verktyg för att prissätta optioner online eller via excel!
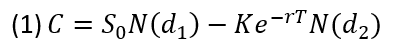
![bsformula2_3 (2) d1 = [ln(S0/K)+(r+(sigma^(2)/2)xT]/sigma^(1/T) (3) d2 =[ln(S0/K)+(r-(sigma^(2)/2)xT]/sigma^(1/T)](https://www.optionspartner.se/wp-content/uploads/2021/09/bsformula2_3.png)
![historical_volatility (2) d1 = [ln(S0/K)+(r+(sigma^(2)/2)xT]/sigma^(1/T) (3) d2 =[ln(S0/K)+(r-(sigma^(2)/2)xT]/sigma^(1/T)](https://www.optionspartner.se/wp-content/uploads/2022/07/historical_volatility.png)
Optionskalkylator (online)
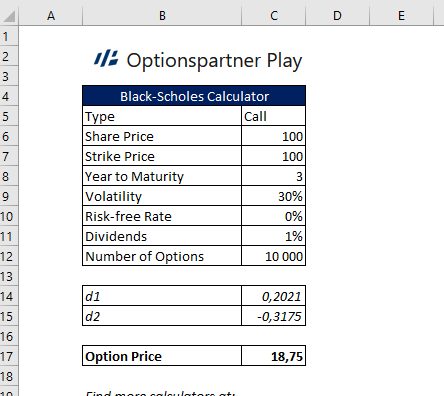
Optionskalkylator (excel)
Hur fungerar Optionskalkylatorn och hur tolkas den?
Förklaring utav de variabler som utgör Black-Scholes Modellen
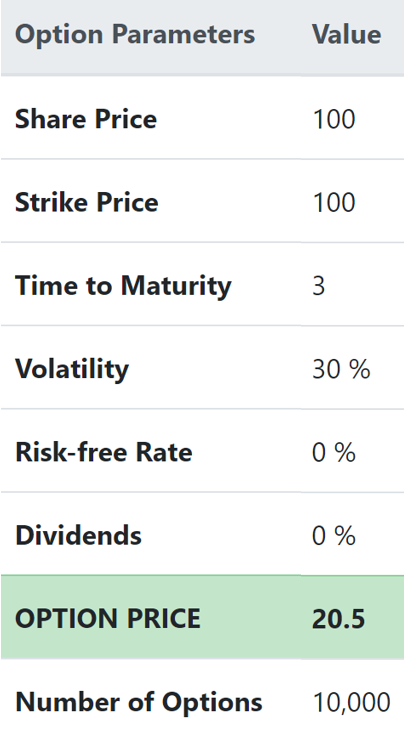
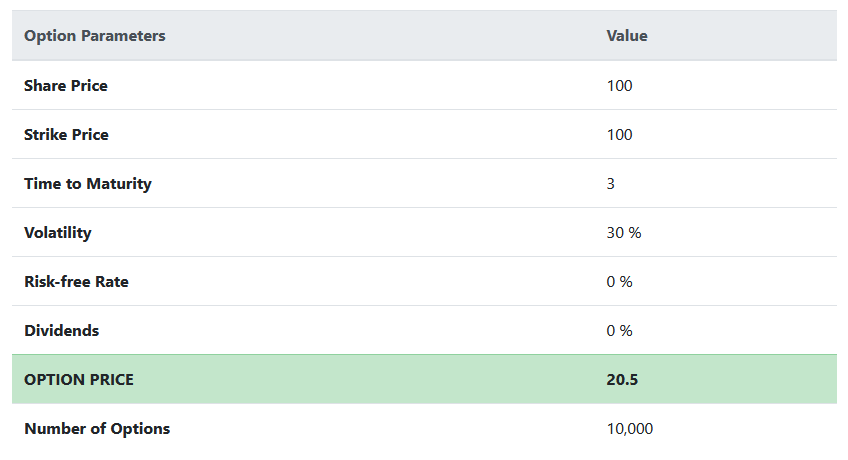
Nedanför finns en som visar de olika variabler i Black-Scholes modellen som avgör vilket värde optionen (rättigheten) representerar. I följande avsnitt förklaras betydelsen av dessa variabler samt hur de påverkar den slutliga optionspremien. Värdena av respektive variabel i bilden är exemplifierat för att underlätta förståelse och i nästkommande avsnitt kommer exemplet studeras närmare.
Förklaring utav de variabler som utgör Black-Scholes Modellen
Värdet av variablerna på bilden åt vänster avgör vilket pris optionen (rättigheten) är värd. Nedan förklaras vad dessa variabler betyder samt hur de påverkar optionspremien.
Option Type - Optionstyp
Long call är den vanligaste typen av option som i svenskt tal motsvaras av en köpoption. Köpoptionen ger dig rättigheten att köpa den underliggande tillgången (aktien) i framtiden till ett förutbestämt pris (striken eller lösenpriset).
Share price - Aktiekursen (initialt)
Den initiala aktiekursen som motsvarar värdet ”idag”. Vilken/vilka dagar som denna skall baseras på samt hur den skall räknas ut bestäms i förtid men måste vara vid datum innan optionerna tecknas.
Strike price - Lösenpris
Lösenpriset är till det pris du har rättighet att köpa aktien i framtiden. Detta bestäms oftast till en procentsiffra av aktiekursen (ex 150% av Share price) men ibland till ett specifikt nummer. Ligger lösenpriset under värdet på aktien vid löptidens slut blir affären lönsam då värdet på aktien du köper överstiger det pris du erlägger. Om istället lösenpriset överstiger aktiekursen bör du inte gå igenom med affären och istället går miste om den premie du betalade vid teckningen av optionen (rättigheten) vid löptidens början. Högre strike (i relation till initial aktiekurs) påverkar optionspremien positivt och minskar kostnaden för rättigheten eftersom högre strike innebär en svårare tröskel för aktiekursen att överstiga om affären i slutändan skall bli lönsam.
Time to Maturity - Löptid
Löptiden är under den period som optionsprogrammet löper. När denna är slut ges tid för optionsinnehavarna att utöva sin rättighet. Detta är normalt sett en period om några veckor eller en månad, men i vissa fall kan teckningsperioden ske i intervall. Exempelvis kan optionsinnehavare få en möjlighet efter 3 år och igen 2 kvartal senare. Längre löptid påverkar optionspremien negativt och ökar kostaden för rättigheten. Detta beror på att om löptiden är längre är sannolikheten för att aktiekursen överstiger lösenpriset större, vilket gör rättigheten mer attraktiv och på så sätt mer värd.
Volatility - Volatilitet
Volatiliteten är ett mått på hur volatil aktiekursen är. Det vill säga hur stora rörelserna är. Högre volatilitet innebär därmed att topparna är högre och dalarna djupare. Som jämförelse har OMXS30 haft strax under 20% volatilitet från mars 2021 och 5 år tillbaka. Högre volatilitet påverkar optionspremien negativt och ökar kostnaden för rättigheten. Anledningen är att desto större rörelserna är i aktiekursen desto större är sannolikheten att aktiekursen under teckningstiden överstiger lösenpriset utan att rörelsen i aktiekursen nödvändigtvis återspeglas i värdet på företaget.
Risk-free Rate - Riskfri ränta
Den riskfria räntan bestäms av den ränta som sätts på statsobligationer, det vill säga garanterad avkastning, utan risk, du kan få genom att köpa en statsobligation samma datum som optionen baseras på (samma dag som bestämmer värdet på aktiekursen inför optionsprogrammet). Den siffra som skrivs in i kalkylatorn motsvarar en statsobligation som är precis lika lång som programmets löptid. Högre riskfri ränta påverkar optionspremien negativt och ökar kostnaden för rättigheten.
Dividends - Utdelning
Utdelning är helt enkelt den mängd utdelning företaget planerar att ge ut till sina aktieägare under löptiden. Denna siffra skrivs i procent och diskonteras till nutid. Högre utdelning under optionsprogrammets löptid påverkar premien positivt och minskar kostnaden för rättigheten. Detta beror på kontrasten av att köpa aktien dag 1 och ta del av utdelningen eller vänta till att (potentiellt) köpa aktien år ex 3.
Number of Options - Antal Optioner
Antal optioner är precis som det låter som; antalet optioner som programmet omfattar. Denna siffra påverkar oftast inte optionspremien, om inte optionerna ger rättighet att teckna sig för nya aktier. Då innebär framtida teckning att antalet aktier späds ut och såväl mängden röster i företaget. Större utspädning påverkar optionspremien negativt och ökar kostnaden för rättigheten.
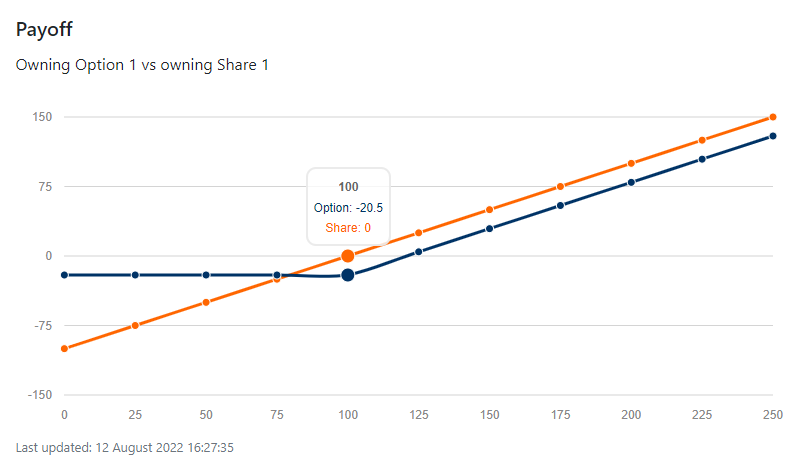
Olika scenarier efter löptidens slut
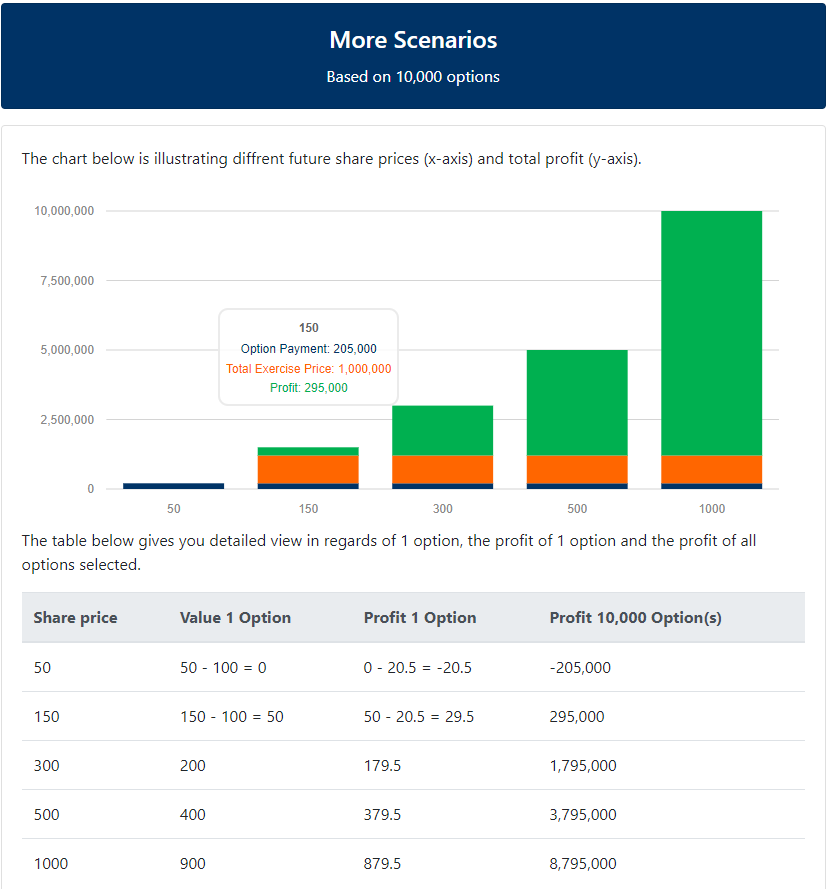
Bilden till vänster visar olika scenarier som kan uppstå efter löptidens slut i form av olika fall av aktiekursen. Grafen och tabellerna bygger på samma siffror som redovisades ovanför i bilden där vi förklarar vad de olika variabler är och hur dessa påverkar priset på optionen.
Olika scenarier efter löptidens slut
Bilden till vänster visar olika scenarier som kan uppstå efter löptidens slut i form av olika fall av aktiekursen. Grafen och tabellerna bygger på samma siffror som redovisades ovanför i bilden där vi förklarar vad de olika variabler är och hur dessa påverkar priset på optionen.
Fall 1 - Aktiekursen ligger på 50 kronor
Om aktiekursen ligger på 50kr år 3 blir förlusten -20,5 (-205,000 för 10 000 optioner). Då kanske första tanken är: ”Om aktiekursen när optionen anskaffades låg på 100 kronor, och kursen har gått ner med 50 kronor, borde väl optionen också gjort det?”. Där är svaret Nej. Det är just det som är det fina med optioner. Du kan inte göra en större förlust än den summa du erlade i början. I detta fall erlades 20,5 kronor för varje option och på samma sätt är det det som utgör förlusten (eftersom du, förhoppningsvis, inte löser in optionerna till aktier).
Fall 2 - Aktiekursen ligger på 150 kronor
I nästa fall har aktiekursen istället gått upp med 50 kronor. Det vi först behöver minnas är lösenpriset (am. strike), vilket låg på 100 kronor. Detta är det pris vi behöver betala om vi vill lösa in optionerna till aktier. När vill vi göra det? Jo, när aktiekursen överstiger lösenpriset, eftersom då anskaffar du en tillgång till ett lägre pris än vad den är värd idag. Vilken vinst är det då vi erhåller? I början erlades 20,5 kronor för optionen och sedan löstes optionen in för 100 kronor till en aktie. Denna aktie är nu värd 150 kronor och vi säljer till det priset. Resultatet 150-(100+20,5) är 29,5 kronor per option och eftersom vi ägde 10 000 optioner blir det slutliga resultatet 295 000 kronor i vinst. Det exempel vi nu gått igenom presenteras även i rutan i grafen över ”150” på x-axeln.
Fall 3 - Lyckligt fall där aktiekursen ligger på 300 kronor
I det tredje fallet ligger aktiekursen på 300 kronor år 3. Detta vill säga kursen har stigit med 200% och även 200 kronor sedan löptidens början. Detta är ett mycket lycklig fall eftersom vinsten uppgår till 179,5 kronor per option. Vilket resulterar i 1 795 000 kronor* efter att alla optioner har lösts in till aktier och därefter sålts.
Dessutom ser vi två andra fall där aktiekursen landat på 500 kronor respektive 1000 kronor. I dessa fall blir vinsten 3 795 000 och 8i795 000 var för sig samt hävstången uppgår till 4,6x och 4,77x för var och en.
* Notera hävstången vi nu upplevt. I Fall 2 där aktiekursen låg på 150 kronor vid löptidens ända och stigit med 50% uppgick vinsten till 295 000 kronor vilket efter initial investering på 205 000 innebär en avkastning på cirka 144% och en hävstång på strax under 3x. I fallet som presenterats hade aktiekursen stigit med 200%. Där uppgick avkastningen till hela 875% vilket genererade en hävstång på cirka 4,4x.
Möjliga följdfrågor efter avsnitten ovan
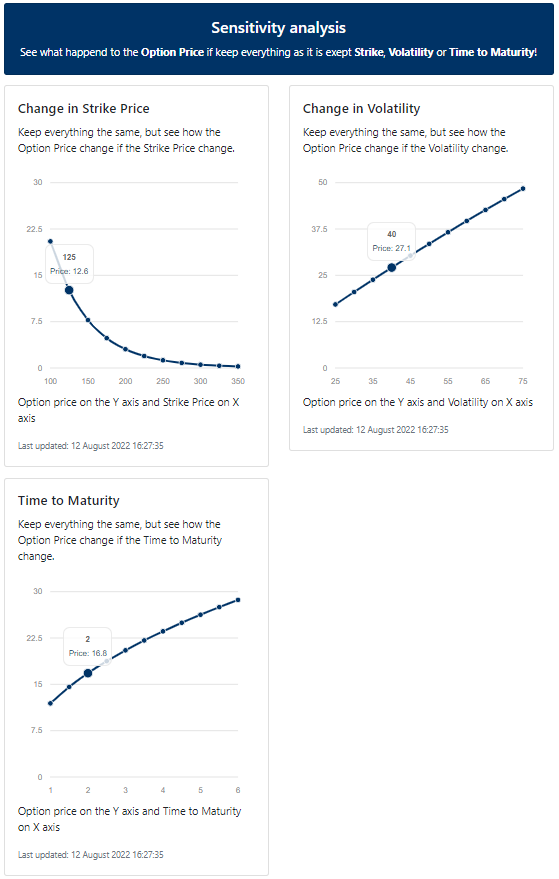
Vad händer om vi ändrar lösenpriset till 200 kronor?
Your content goes here. Edit or remove this text inline or in the module Content settings. You can also style every aspect of this content in the module Design settings and even apply custom CSS to this text in the module Advanced settings.
Lästips:
Vårt bibliotek - en nyttig källa till trygg informationEn välbeprövad metod
Anekdotiska bevis om finansiella verktyg som påminner om optioner kan spåras tillbaka till 580 f. Kr. »
Agentproblemet
Varför inför företag incitamentsprogram? Agentproblemet ger svar. »
Testa vår Black & Scholes-kalkylator
Sätt pris på din option med vårt enkla verktyg! Testa gratis på: play.optionspartner.com »
17 ekvationer som förändrade världen
Från Newtons gravitationslag till Black-Scholes-modellen som används av bankirer för att förutsäga marknaderna, ekvationer finns överallt – och de är grundläggande för vardagen.
Black-Scholes formel med exempel
Black-Scholes-Merton-formelns anatomi.